Unraveling the Domain and Range of Graphs – A Worksheet Guide

Have you ever gazed at a graph and wondered, “What’s the story it’s telling me? What are its limits?” Understanding the domain and range of a graph is like unlocking the secrets of a mathematical language. It helps us decipher the boundaries of the function, revealing the values the graph can take on and the inputs it can accept. This is essential knowledge for anyone venturing into the world of mathematics and its applications.

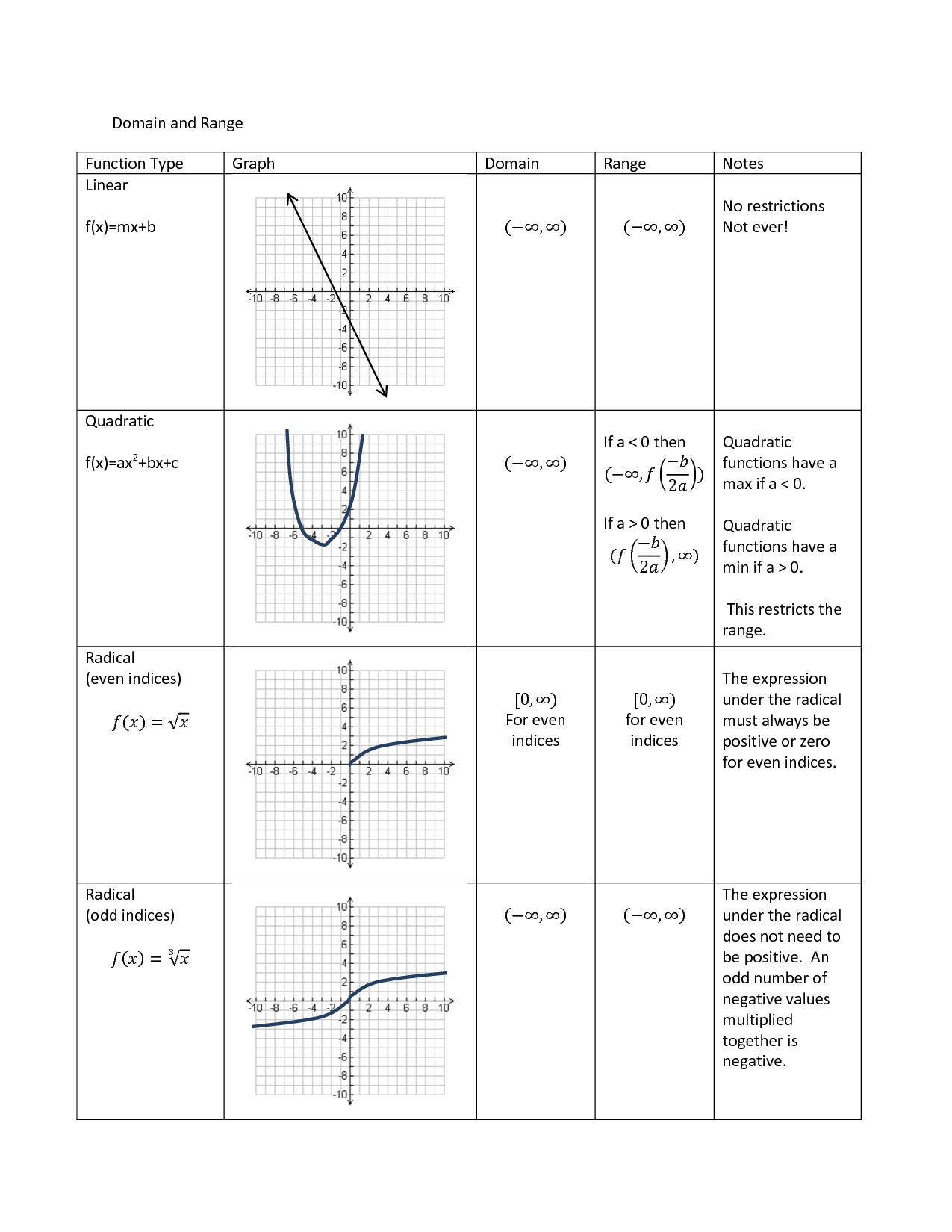
Image: materialdbgale.z13.web.core.windows.net

In this guide, we’ll embark on a journey through the realm of domain and range, focusing on how to decipher these concepts from graphs themselves. We’ll demystify the process, explore various types of graphs, and equip you with the confidence to tackle even the most challenging domain and range worksheets.

Defining the Realm: What is Domain and Range?

Imagine a graph as a map of a function’s behavior. The domain represents all possible input values along the horizontal axis (the x-axis). It’s the set of all numbers you could plug into the function. On the other hand, the range encompasses all possible output values, residing along the vertical axis (the y-axis). It’s the set of all the numbers you can get as answers after applying the function.

To visualize this:

• Domain: Think of it as the set of all possible “addresses” in your graph.
• Range: Consider it as the set of all possible “values” or “outcomes” at those addresses.

Decoding the Graph: Mastering Domain and Range

Let’s dive into the practical aspect of finding the domain and range from graphs. Here’s a step-by-step approach for various graph types:

1. Linear Graphs: A Straightforward Path

Linear graphs, with their straight lines, often have a simple domain and range.

• Domain: Typically, the domain of a linear function extends infinitely in both directions along the x-axis, meaning all real numbers are valid inputs. You can represent this as (-∞, +∞).
• Range: Similarly, the range also extends infinitely, covering all real numbers along the y-axis, represented as (-∞, +∞).

Example: Consider the equation y = 2x + 1. Its graph is a straight line that extends forever in both directions. So, both the domain and range are (-∞, +∞).

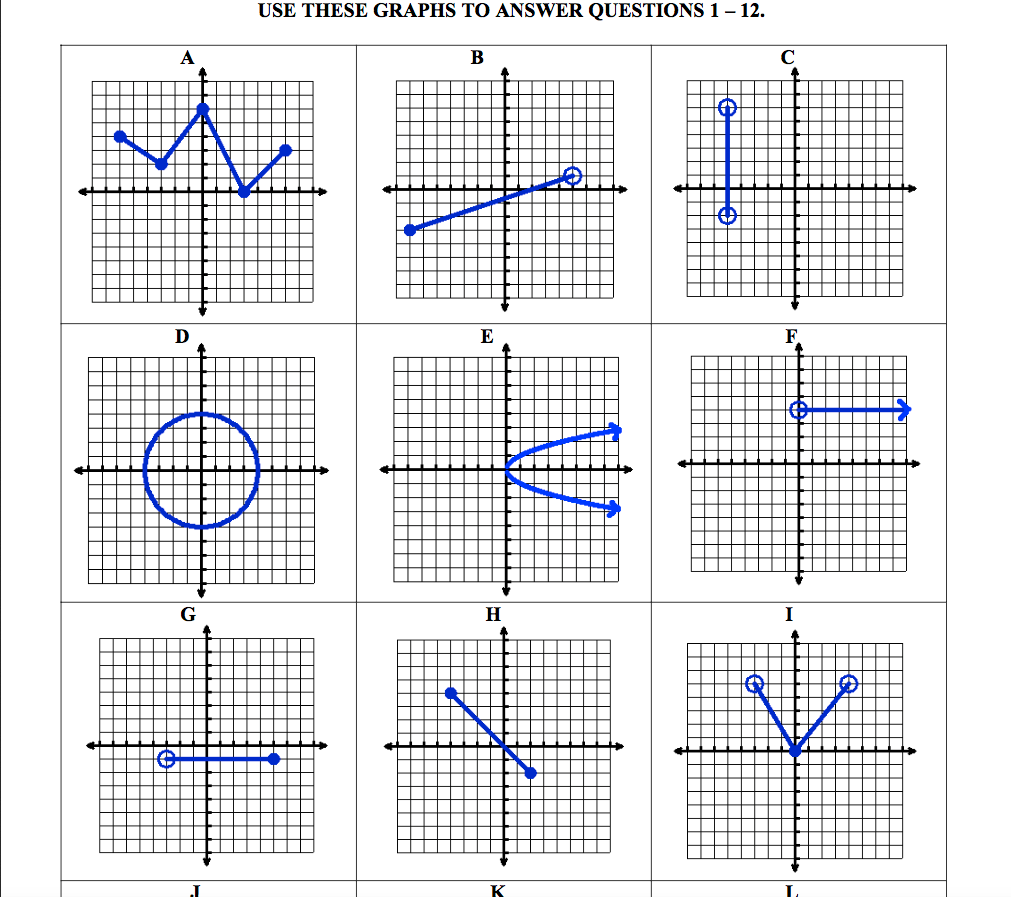
Image: quizizz.com

2. Quadratic Graphs: Parabolas with Boundaries

Quadratic graphs take the shape of a parabola, and their domain and range can be slightly more complex.

• Domain: Like linear graphs, quadratic functions typically have a domain of (-∞, +∞).

• Range: However, the range might vary depending on whether the parabola opens upwards or downwards.

  • If the parabola opens upwards, the range starts at the y-coordinate of the vertex (lowest point) and extends to positive infinity: [vertex’s Y-coordinate, +∞).
  • If the parabola opens downwards, it’s the opposite: the range starts at negative infinity and extends to the y-coordinate of the vertex: (-∞, vertex’s Y-coordinate].

Example: Let’s take the quadratic equation y = x² – 2x + 1. Its graph is a parabola that opens upwards. Its vertex is (1, 0), meaning the range is [0, +∞).

3. Exponential Graphs: A Growing Curve

Exponential graphs are characterized by their curves that grow rapidly.

• Domain: These graphs usually have a domain of (-∞, +∞), as the x-axis can accommodate any input value.

• Range: The range depends on the presence of a horizontal asymptote (a line that the function approaches but never touches).

  • Without asymptote: The range is (-∞, +∞).
  • With asymptote: The range is either (-∞, asymptote’s Y-coordinate) or (asymptote’s Y-coordinate, +∞), based on whether the curve approaches the asymptote from below or above.

Example: Consider the exponential function y = 2^x. Its graph doesn’t have a horizontal asymptote and extends infinitely upwards. The domain is (-∞, +∞), while the range is (0, +∞).

4. Absolute Value Graphs: The V-shaped Deformity

Absolute value graphs produce distinctive V-shaped patterns.

• Domain: The domain is usually (-∞, +∞), as the x-axis can contain inputs from both positive and negative sides.

• Range: The range depends on the position of the vertex.

  • Vertex at (0, 0): The range is [0, +∞).
  • Vertex shifted upwards or downwards: The range is (vertex’s Y-coordinate, +∞) or (-∞, vertex’s Y-coordinate), respectively.

Example: Take the absolute value function y = |x|. Its graph is a V-shaped curve with its vertex at (0, 0). The domain is (-∞, +∞), and the range is [0, +∞).

5. Radical Graphs: Restricted Domains and Ranges

Graphs involving radical expressions (like square roots) often have restricted domains and ranges.

• Domain: The domain is determined by the radicand (the expression under the radical). The radicand cannot be negative in the case of even roots (like square roots). You need to find the values of x that make the radicand non-negative.
• Range: The range depends on the type of radical and the transformations applied to the expression.

Example: The function y = √(x – 2) has a domain of [2, +∞), as the radicand x – 2 must be non-negative. The range is [0, +∞) because the square root function produces only non-negative outputs.

Going Beyond: Domain and Range in Real-World Applications

Understanding domain and range isn’t just about solving worksheet problems. It forms the foundation for analyzing real-world phenomena that can be modeled using mathematical functions.

• Finance: When analyzing stock prices, the domain might represent time (input), and the range represents stock value (output). The range tells us the possible price fluctuations over that time period.
• Physics: In projectile motion, the domain could represent the launch angle (input), and the range could represent the distance traveled (output). Understanding this range helps predict how far an object will go based on its launch angle.
• Engineering: When designing bridges or buildings, engineers consider the domain of possible load forces (input) and aim to ensure the range of structural stresses (output) remains within safe limits.

Domain and Range Worksheets: A Stepping Stone to Mastery

Domain and range worksheets provide invaluable practice in applying these concepts to various types of graphs. They help you develop a deeper understanding of the relationship between a function and its representation on a graph.

Here’s how you can make the most of domain and range worksheets:

1. Focus on Visualizing: Instead of just memorizing rules, focus on visualizing the graph and understanding how the shape dictates the domain and range.
2. Identify Key Features: Look for important features like the vertex, asymptotes, and intercepts, as they often provide clues about the domain and range.
3. Practice with Different Graph Types: Work on worksheets that cover various functions, including linear, quadratic, exponential, absolute value, and radical graphs.
4. Seek Explanation: If you get stuck on a problem, don’t hesitate to ask for help or seek explanations online. Understanding the reasoning behind the answer is crucial.
5. Review and Reflect: After completing a worksheet, review your solutions. Identify any patterns you’ve noticed and reflect on where you might need further practice.

Domain And Range Of Graphs Worksheet Answers

Conclusion: Unlocking the Language of Graphs

The ability to determine domain and range from graphs is a valuable mathematical skill that unlocks deeper insights into the behavior of functions. By mastering this concept, you gain a powerful tool for understanding the limits, boundaries, and potential of various phenomena that can be represented graphically. So, embark on this journey of discovering domain and range—you’ll be amazed at how much you can uncover!