Have you ever wondered how mapmakers determine the exact distance between two cities? Or how architects plan the precise placement of walls and windows in a building? The answer lies in the fundamental concept of line segments and distance, which are the building blocks of geometry and have practical applications in many fields.
Image: slidetodoc.com
This comprehensive guide will delve into the world of line segments and distance, exploring their definitions, properties, and methods for calculating distance. We’ll provide a detailed answer key for practice exercises, helping you master this essential mathematical skill. Whether you’re a student preparing for a geometry test or simply curious about the underlying principles behind spatial measurements, this article will empower you with a deeper understanding of line segments and distance.
Understanding Line Segments
A line segment is a straight path connecting two distinct points, known as the endpoints. It’s a fundamental geometric shape that forms the basis of more complex figures. Imagine a ruler; the markings on a ruler represent line segments. Each line segment on the ruler has a starting point and an ending point.
In geometry, line segments are represented by a single line with two points marked on the ends. For example, line segment AB would be written as AB, where A and B are the endpoints.
Measuring the Distance Between Points
The distance between two points is the length of the line segment connecting them. It’s a concept we use daily, from measuring the length of a room to navigating a road trip. To calculate distance, we need a unit of measurement, such as inches, centimeters, or miles.
Using a Ruler
The most basic tool for measuring distance is a ruler. Rulers have markings that represent units of measurement. To find the distance between two points, you simply place the ruler on the line segment, aligning the zero mark with the starting point and reading the mark that aligns with the endpoint.
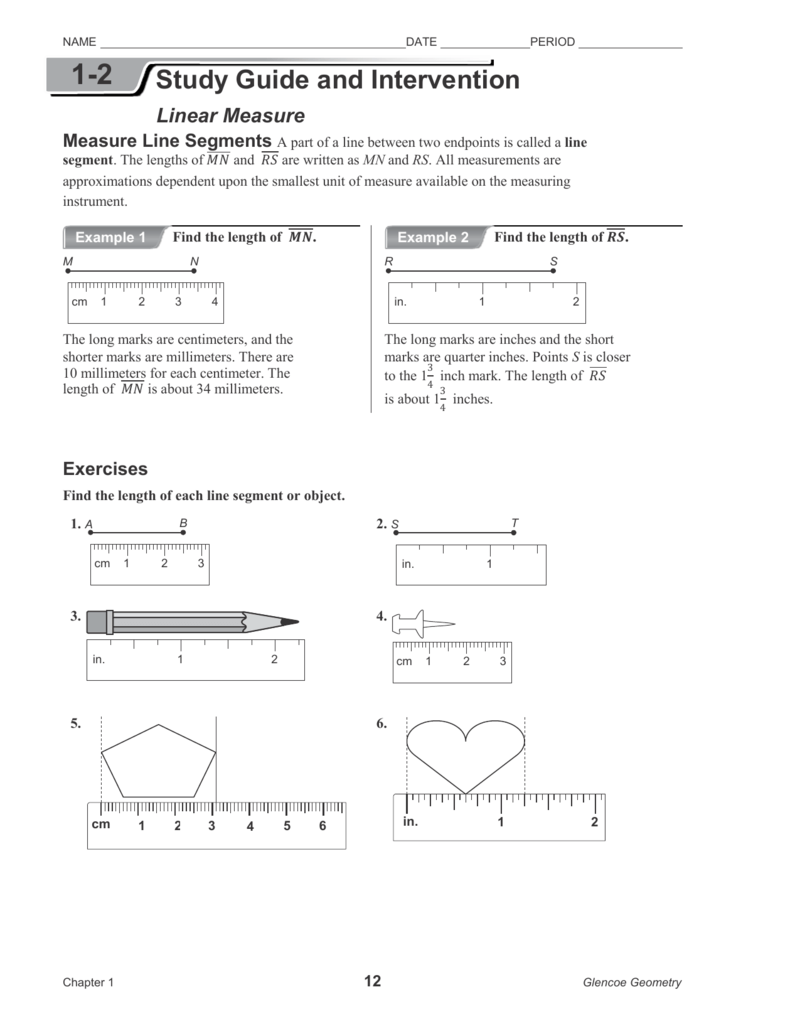
Image: alaina-chapter.blogspot.com
Using the Distance Formula
For more complex scenarios, we can use the distance formula, a mathematical equation derived from the Pythagorean theorem. The distance formula is:
Distance = √( (x2 – x1)2 + (y2 – y1)2 )
Where:
- (x1, y1) represents the coordinates of the first endpoint.
- (x2, y2) represents the coordinates of the second endpoint.
Practice Exercises: Line Segments and Distance
Now that we understand the basics, let’s work through some practice exercises to solidify our understanding of line segments and distance.
Exercise 1: Identifying Endpoints
Instruction: Identify the endpoints of the line segment shown below.
[Insert Image: A line segment with points labeled A and B]
Answer: The endpoints of the line segment are A and B.
Exercise 2: Calculating Distance Using a Ruler
Instruction: Use a ruler to measure the length of the line segment shown below.
[Insert Image: A line segment with a clear length marked in inches or centimeters.]
Answer: [The actual length of the line segment in inches or centimeters].
Exercise 3: Calculating Distance Using the Distance Formula
Instruction: Calculate the distance between points A (2, 3) and B (5, 7) using the distance formula.
Answer:
Distance = √( (5 – 2)2 + (7 – 3)2 )
Distance = √( 32 + 42 )
Distance = √( 9 + 16 )
Distance = √25
Distance = 5
Therefore, the distance between points A and B is 5 units.
Exercise 4: Real-World Application
Instruction: On a map, two cities are located 5 centimeters apart. If the map scale is 1 cm = 20 km, what is the actual distance between the two cities?
Answer:
Since 1 cm on the map represents 20 km in reality, 5 cm on the map would represent 5 * 20 = 100 km.
Therefore, the actual distance between the two cities is 100 kilometers.
Important Considerations
Here are some important aspects to consider when working with line segments and distance:
- Units: Always pay attention to the units of measurement used. If the problem involves different units, convert them to a common unit before performing calculations.
- Precision: The level of precision required for distance measurements depends on the context. For rough estimations, rounding to the nearest whole number might suffice, while for precise engineering calculations, measurements may need to be accurate to several decimal places.
- Applications: Understanding line segments and distance is crucial in fields such as architecture, construction, navigation, computer graphics, and mapmaking. It’s a foundational concept that underlies many real-world applications.
1 2 Practice Line Segments And Distance Answer Key
Conclusion
By understanding the concepts of line segments and distance, we can unlock a deeper appreciation for the world around us. From measuring the space in our homes to navigating across continents, the principles we’ve explored are essential for making sense of our environment. We encourage you to continue exploring geometry and its practical applications. The possibilities are endless!






